How to get a path to the desktop for current user in C Each month, over 5. Stack Overflow to learn, share their knowledge, and build their careers. M10-spikey.png' alt='Mathematica 10.1' title='Mathematica 10.1' />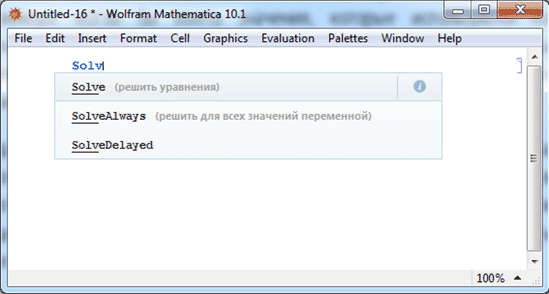Join the worlds largest developer community. MathWorld Headline News Mathematicas Google Aptitude By Ed Pegg Jr. Eric W. Weisstein With additional contributions by Daniel Lichtblau, Adam Strzebonski, Oyvind. Specialized quantiles. Some qquantiles have special names citation needed The only 2quantile is called the median The 3quantiles are called tertiles or. FINAL REPORT. Understanding the Effect of KIPP as it Scales Volume I, Impacts on Achievement and Other Outcomes. Final Report of KIPPs Investing in Innovation. Occ Stock Loan Hedge Program. Mathematica 10.1' title='Mathematica 10.1' />Quantile Wikipedia. Probability density of a normal distribution, with quartiles shown. The area below the red curve is the same in the intervals ,Q1, Q1,Q2, Q2,Q3, and Q3,. In statistics and the theory of probability, quantiles are cutpoints dividing the range of a probability distribution into contiguous intervals with equal probabilities, or dividing the observations in a sample in the same way. There is one less quantile than the number of groups created. Thus quartiles are the three cut points that will divide a dataset into four equal size groups cf. Common quantiles have special names for instance quartile, decile creating 1. The groups created are termed halves, thirds, quarters, etc., though sometimes the terms for the quantile are used for the groups created, rather than for the cut points. Quantiles are values that partition a finite set of values into q subsets of nearly equal sizes. There are q 1 of the q quantiles, one for each integer k satisfying 0 lt k lt q. In some cases the value of a quantile may not be uniquely determined, as can be the case for the median 2 quantile of a uniform probability distribution on a set of even size. Quantiles can also be applied to continuous distributions, providing a way to generalize rank statistics to continuous variables. When the cumulative distribution function of a random variable is known, the q quantiles are the application of the quantile function the inverse function of the cumulative distribution function to the values 1q, 2q, q 1q. Specialized quantileseditSome q quantiles have special names citation neededQuantiles of a populationeditAs in the computation of, for example, standard deviation, the estimation of a quantile depends upon whether one is operating with a statistical population or with a sample drawn from it. For a population, of discrete values or for a continuous population density, the k th q quantile is the data value where the cumulative distribution function crosses kq. That is, x is a k th q quantile for a variable X if. PrX lt x kq or, equivalently, PrX x 1 kqand. PrX x kq or, equivalently, PrX x 1 kq. For a finite population of N equally probable values indexed 1, N from lowest to highest, the k th q quantile of this population can equivalently be computed via the value of Ip Nkq. If Ip is not an integer, then round up to the next integer to get the appropriate index the corresponding data value is the k th q quantile. On the other hand, if Ip is an integer then any number from the data value at that index to the data value of the next can be taken as the quantile, and it is conventional though arbitrary to take the average of those two values see Estimating the quantiles. If, instead of using integers k and q, the p quantile is based on a real numberp with 0 lt p lt 1 then p replaces kq in the above formulae. Some software programs including Microsoft Excel regard the minimum and maximum as the 0th and 1. ExampleseditThe following two examples use the Nearest Rank definition of quantile with rounding. For an explanation of this definition, see percentiles. Even sized populationeditConsider an ordered population of 1. What are the 4 quantiles the quartiles of this datasetQuartile. Calculation. Result. Zeroth quartile. Although not universally accepted, one can also speak of the zeroth quartile. This is the minimum value of the set, so the zeroth quartile in this example would be 3. First quartile. The rank of the first quartile is 1. The third value in the population is 7. Second quartile. The rank of the second quartile same as the median is 1. Third quartile. The rank of the third quartile is 1. The eighth value in the population is 1. Fourth quartile. Although not universally accepted, one can also speak of the fourth quartile. This is the maximum value of the set, so the fourth quartile in this example would be 2. Under the Nearest Rank definition of quantile, the rank of the fourth quartile is the rank of the biggest number, so the rank of the fourth quartile would be 1. So the first, second and third 4 quantiles the quartiles of the dataset 3, 6, 7, 8, 8, 1. If also required, the zeroth quartile is 3 and the fourth quartile is 2. Odd sized populationeditConsider an ordered population of 1. What are the 4 quantiles the quartiles of this dataset Quartile. Calculation. Result. Zeroth quartile. Although not universally accepted, one can also speak of the zeroth quartile. This is the minimum value of the set, so the zeroth quartile in this example would be 3. First quartile. The first quartile is determined by 1. The third value in the population is 7. Second quartile. The second quartile value same as the median is determined by 1. Therefore, 6 is the rank in the population from least to greatest values at which approximately 24 of the values are less than the value of the second quartile or median. The sixth value in the population is 9. Third quartile. The third quartile value for the original example above is determined by 1. The ninth value in the population is 1. Fourth quartile. Although not universally accepted, one can also speak of the fourth quartile. This is the maximum value of the set, so the fourth quartile in this example would be 2. Under the Nearest Rank definition of quantile, the rank of the fourth quartile is the rank of the biggest number, so the rank of the fourth quartile would be 1. So the first, second and third 4 quantiles the quartiles of the dataset 3, 6, 7, 8, 8, 9, 1. If also required, the zeroth quartile is 3 and the fourth quartile is 2. Estimating quantiles from a sampleeditWhen one has a sample drawn from an unknown population, the cumulative distribution function and quantile function of the underlying population are not known and the task becomes that of estimating the quantiles. There are several methods. Mathematica,2Matlab,3R4 and GNU Octave5 programming languages include nine sample quantile methods. SAS includes five sample quantile methods, Sci. Py6 and Maple7 both include eight, EViews8 includes the six piecewise linear functions, STATA includes two, and Microsoft Excel includes two. Mathematica supports an arbitrary parameter for methods that allows for other, non standard, methods. In effect, the methods compute Qp, the estimate for the k th q quantile, where p kq, from a sample of size N by computing a real valued index h. When h is an integer, the h th smallest of the N values, xh, is the quantile estimate. Otherwise a rounding or interpolation scheme is used to compute the quantile estimate from h, xh, and xh. For notation, see floor and ceiling functions. The estimate types and interpolation schemes used include Typeh. Qp. Notes. R 1, SAS 3, Maple 1. Np 12xh 12Inverse of empirical distribution function. When p 0, use x. R 2, SAS 5, Maple 2. Np 12xh 12 xh 12 2. The same as R 1, but with averaging at discontinuities. When p 0, use x. When p 1, use x. N. R 3, SAS 2. NpxhThe observation numbered closest to Np. Here, h indicates rounding to the nearest integer, choosing the even integer in the case of a tie. When p 12 N, use x. R 4, SAS 1, Sci. Py 0,1, Maple 3. Npxh h h xh 1 xhLinear interpolation of the empirical distribution function. When p lt 1 N, use x. When p 1, use x. N.